- 《计算几何:算法与应用》pdf
- 本书网站 geobook 提供了本书各版本的勘误、所有插图、所有算法的伪代码，以及其它资源。
1.计算几何:导言
为了说明在几何算法的建立过程中所出现的问题，本节将讨论平面凸包的计算。
1.1.凸包的例子
凸包：凸包中的任意两点的连线段在凸包内部。
在计算机科学和数学中，退化情况（Degenerate Case）指的是问题或情况变得异常简单或特殊，以至于常规的算法或方法无法适用或失去有效性。在这种情况下，问题的某些参数或条件会导致解决方案变得不明确、不唯一或无法得到正确的结果。
计算凸包的朴素算法：
- 退化情况：相对于由p和q所确定的直线，一个点r的位置并不是非左即右，有可能正好落在这条直线上。
- 舍入误差：由于计算过程中是浮点运算，必然存在舍入误差，影响测试精度。
- 时间复杂度为 $\mathcal{O}(n^3)$。
计算凸包的递增式策略：
按x坐标从左至右遍历顶点，计算出构成上凸包(upper hull)的那些顶点，再自右向左扫描，计算出下凸包(lower hull)。
若按照顺时针方向沿着多边形的边界行进，则在每个顶点处都要改变方向。若是凸多边形，则必然每次都是向右转。令$l_{upper}$为从左向右存放上凸包各顶点的一个列表，将$p_i$接在$l_{upper}$最后，再检查$l_{upper}$中最末尾的三个点，看它们是否构成一个右拐(right-turn)，若不是，就必须将中间的(即倒数第二个)顶点从上凸包中剔除出去。
- 当点x坐标相同时，按照y坐标对它们排序。
- 退化情况：将共线的点看成是构成一个左拐。
- 时间复杂度为 $\mathcal{O}(n\log n)$。
2.线段求交:专题图叠合
为了增加地图的可读性，地理信息系统将（不同类型的）信息划分为若干层（layer），每一层都是一幅专题图（thematic map）。这样，某一层可能负责存储有关公路的信息，第二层存放的可能是所有城市的信息，而另一层则存放河流的信息，诸如此类。
2.1.线段求交
我们首先讨论地图叠合问题的最简单形式。相互叠合的两个地图层，分别都是由一组线段表示的某个网络，如道路、铁路、河流。
依次检查每一对线段是否相交需要$\mathcal{O}(n^2)$时间。
为避免对所有的线段对进行测试，考虑只有那些相互靠近的线段，才可能相交，相距甚远的线段不可能相交。
首先可以通过投影，排除不可能相交的线段对。相当于用一条假想直线 $l$ 自上而下扫过整个平面，跟踪记录所有与之相交的线段，以找出所需的所有线段对。这类算法被称为平面扫描算法(plane sweep algorithm)，其中使用到的直线 $l$ 被称为扫描线(sweep line)。与当前扫描线相交的所有线段构成的集合，被称为扫描线的状态(status)。只有在某些特定的位置，才需要对扫描线的状态进行更新，我们称这些位置为平面扫描算法的事件点(event point)。就本算法而言，这里的事件点就是各线段的端点。只有在扫描线触及某个事件点的时候，算法才会进行实质的处理⎯⎯更新扫描线的状态，并进行一些相交测试。
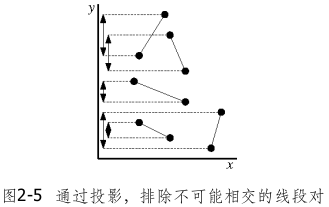
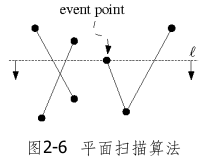
与同一扫描线相交的两条线段，在水平方向上仍然有可能相距很远。我们可以沿着扫描线，将与之相交的所有线段自左向右排序。只有当其中的某两条线段沿水平方向相邻时，才需要对其进行测试。
在任一时刻，状态结构中的所有线段之间具有一个定义明确的次序，因此可以使用一棵平衡二分查找树来实现状态结构。
2.2.双向链接边表
一般的地图，要将整个平面划分为多个子区域。我们将用双向链接边表（doubly-connected edge list）表示子区域划分。
将每条边的两边分别视为一条半边（half-edge），它们互为孪生兄弟（twin）。这样任何一条半边都有唯一的前驱半边和后继半边。则每条半边就只隶属于唯一一张面的边界。
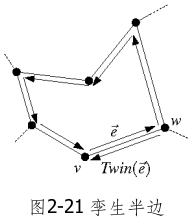
在为每一条半边指定后继半边时，总是依照同一原则：后继半边的方向，应该能够沿逆时针方向遍历其对应的面。这样也同时为各条半边导出了一个方向：如果观察这沿着这一方向前行，每条半边所参与围成的那张面，总是位于其左侧。（小车将靠右行驶）
若是空洞，就按顺时针方向来遍历其边界。这样，无论是哪张面，对于构成其边界的那些半边来说，该面总是位于其左侧。
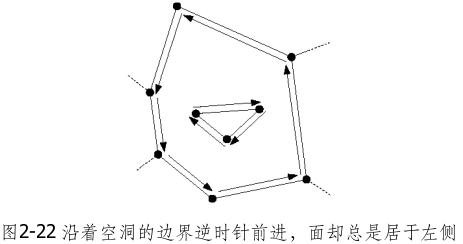
双向链接边表由三组记录构成，分别对应于顶点、面、半边。
- v顶点相关：顶点的坐标Coordinates(v)、指向以该顶点为起点的某条半边的指针IncidentEdge(v)
- f面相关：指向该面外边界(outer boundary)上的任意一条半边的指针OuterComponent(f)、指向该面的各个空洞的边界上的某一条半边的指针列表InnerComponents(f)
- e半边相关：指向该半边起点的指针Origin(e)、指向其孪生半边的指针Twin(e)、指向其参与围成的那张面的指针IncidentFace(e)、指向其沿着IncidentFace(e)边界的前驱边Prev(e)与后继边Next(e)
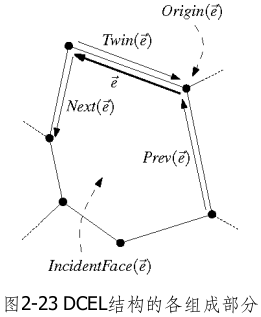
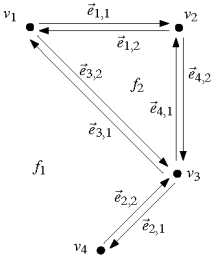
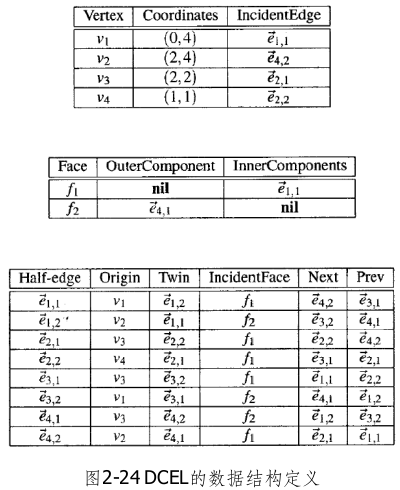
在双向链接边表的某些实现中，可能还会要求子区域划分的顶点和边所对应的图必须是连通的。为此，只需引入一些虚边（dummy edge）。保证连通性至少有两个好处：首先，只需一趟图遍历，就可以访问到所有的半边；另外，既然连通图对应的子区域划分绝不会出现空洞，InnerComponents()列表也就不必存在了。
3.多边形三角剖分:画廊看守
3.1.看守与三角剖分
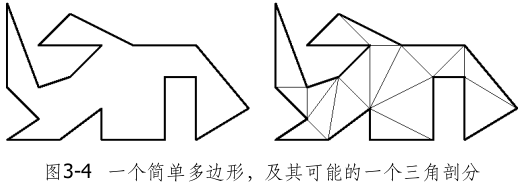定理 3.1：任何简单多边形都存在（至少）一个三角剖分；若其顶点数目为n，则它的每个三角剖分都恰好包含n-2个三角形。
定理 3.2（艺术画廊定理）：包含n个顶点的任何简单多边形，只需（放置在适当位置的）$\lfloor \frac n3 \rfloor$台摄像机就能保证：其中任何一点都可见于至少一台摄像机。
定理 3.3：任给一个包含n个顶点的简单多边形P。总可以在O(nlogn)时间内，在P中确定$\lfloor \frac n3 \rfloor$台摄像机的位置，使得P中的任何一点都可见于其中的至少一台摄像机。
3.2.多边形的单调块划分
如果对任何一条垂直于l的直线l’，l’与该多边形的交都是连通的，那么这个简单多边形关于直线l单调（monotone with respect to a line l）。
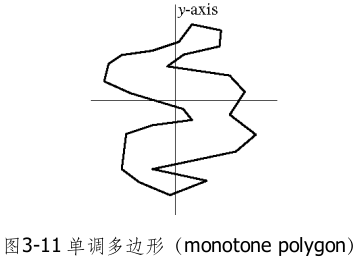
例如y-单调多边形（y monotone polygon）的特性：在沿着多边形的左（右）边界，从最高顶点走向最低顶点的过程中，我们始终都是朝下方（或者水平）运动，而绝不会向上。
我们对多边形P进行三角剖分的策略是：首先将P划分成若干个y-单调块，然后再对每块分别进行三角剖分。
P的顶点可划分为五类：
- 起始顶点(start vertex)：与它相邻的两个顶点的高度都比它低，而且在顶点v处的内角小于π
- 分裂顶点(split vertex)：该内角大于π
- 终止顶点(end vertex)：与它相邻的两个顶点的高度都比它高，而且在v处的内角小于π
- 汇合顶点(merge vertex)：该内角大于π
- 普通顶点(regular vertex)：这四类拐点以外的所有顶点。也就是说，在每个普通顶点的两个相邻顶点中，必然有一个比它高，而另一个则比它低。
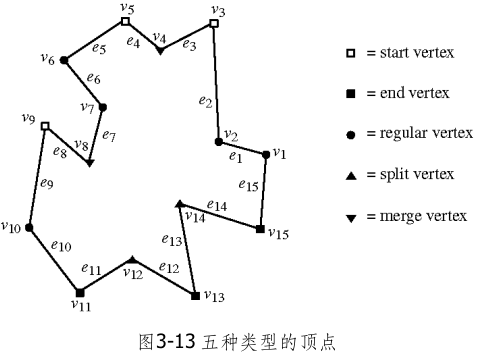
引理 3.4：一个多边形若既不含分裂顶点，也不含汇合顶点，则必然是y-单调的。
引理 3.5：通过引入一系列互不相交的对角线，算法MAKE MONOTONE能够将P划分为多个单调子多边形。
定理 3.6：使用O(n)的存储空间，可以在O(nlogn)时间内将包含n个顶点的任何简单多边形分解为多个y-单调的子块。
7.Voronoi图:邮局问题
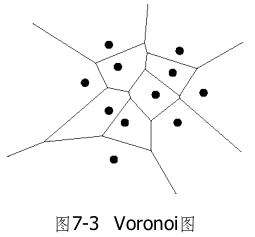
维诺图（Voronoi图）是基于给定一组基点的空间分割。它将平面分割成一组多边形，每个多边形包围一个基点，该多边形中的每个点距离最近的基点比其他基点更近。每条边都是某对基点连线的垂直平分线的一段。
7.3.线段集Voronoi图
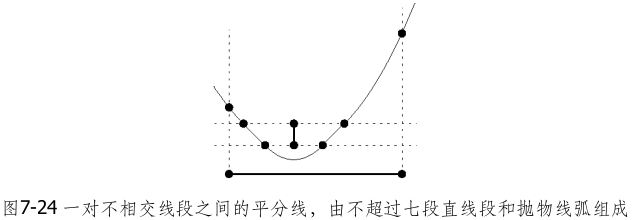
点以外的其它物体也可定义Voronoi图。此时，平面上一点到物体的距离，定义为该点到物体上各点的最近距离。两点之间的平分线必是一条直线，但不相交线段之间的平分线的形状却要更为复杂。它最多可分为七段，每一段或是直线段，或是抛物线弧（parabolic arc）。若到一条线段的最短距离在其某个端点达到，而到另一条线段的最短距离却是在其内部某点达到，则对应于一条抛物线弧。其它的情况下，都对应于一条直线段。
线段集Voronoi图的一个应用实例即运动规划（motion planning，参见第13章）。假设给定可表示为n条线段的一组障碍物和一个机器人R，该机器人可以近似为一个包围圆D（enclosing disk），可以朝任意方向自由移动。需要在两个位置之间，为该机器人找出一条无冲突的运动路径（collision-free motion），或者判定无路可通。
运动规划的技巧之一，就是所谓的收缩（retraction）。其思路是：Voronoi图中的各条弧给出了介于各线段基点之间的中间线，沿这些弧行进遇到障碍的可能性最小，因此其对应的路线也是最好的无冲突运动路径。下图给出了一个矩形区域内的一组线段，以及与它们相对应的Voronoi图。
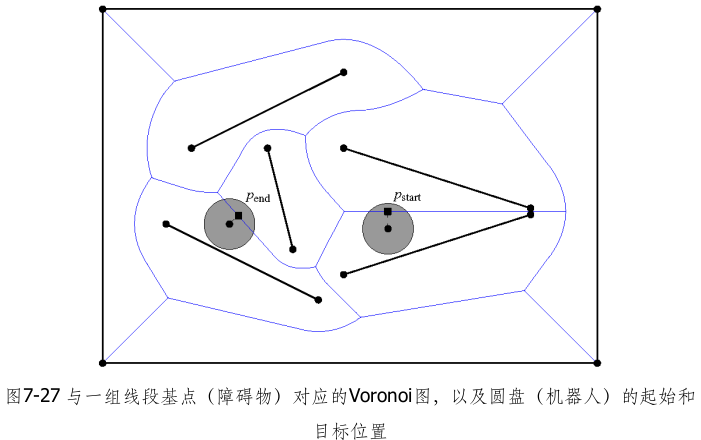
采用以下算法，即可在由任意一组线段表示的障碍物之间，规划出一条无冲突的运动路径。
