第10讲 后端1
10.1 概述
10.1.1 状态估计的概率解释
SLAM中的图像有时间上的先后顺序,而SfM中允许使用完全无关的图像。
我们假设状态量和噪声项服从高斯分布——这意味着在程序中只需要储存它们的均值和协方差矩阵即可。
由于位姿和路标点都是待估计的变量,我们改变一下记号,令$x_k$为k时刻的所有未知量。它包含了当前时刻的相机位姿与m个路标点。在这种记号的意义下(虽然与之前稍有不同,但含义是清楚的),写成:$x_k\triangleq{x_k,y_1,\cdots,y_m }$。同时,把k时刻的所有观测记作$z_k$。于是,运动方程与观测方程的形式可写得更加简洁。这里不会出现y,但我们心里要明白这时x中已经包含了之前的y:
$ 运动方程:\ \ x_k=f(x_{k-1},u_k)+w_k \tag{1} $
$ 观测方程:\ \ z_k=h(x_k)+v_k \tag{2} $
如何对状态进行估计。按照贝叶斯法则,把$z_k$与$x_k$交换位置,有:
$ P(x_k |x_0,u_{1:k},z_{1:k})\propto P(z_k|x_k)P(x_k|x_0,u_{1:k},z_{1:k-1}) \tag{3} $
10.1.2 线性系统和KF
由于马尔可夫性,k时刻状态只与k-1时刻有关,与k-1之前的无关。所以可简化为只与$x_{k-1}$和$u_k$有关的形式。
假设系统为线性高斯系统,即运动方程和观测方程可以用线性方程来描述,所有状态和噪声满足高斯分布:
$ 运动方程:\ \ x_k=Ax_{k-1}+u_k+w_k,\ \ \ \ w_k\sim N(0,R) \tag{4} $
$ 观测方程:\ \ z_k=C_kx_k+v_k,\ \ \ \ v_k\sim N(0,Q) \tag{5} $
现在的任务是:已知k-1时刻的后验状态估计$\hat{x_{k-1}}$及其协方差$\hat{P_{k-1}}$,根据k时刻的输入$u_k$和观测数据$z_k$,确定$x_k$的后验分布。(用$\hat{x}_k$表示后验,用$\bar{x}_k$表示先验)
第一步是通过运动方程确定$x_k$的先验分布。根据高斯分布的性质有(6),这一步称为预测,显示了如何从上一个时刻的状态,根据输入信息推断当前时刻的状态分布。
$ P(x_k |x_0,u_{1:k},z_{1:k-1})=N(A_k\hat{x}_{k-1}+u_k, A_k\hat{P}_kA^T_k+R) \tag{6} $
记: $ \bar{x_k}=A_k\hat{x_{k-1}}+u_k,\ \ \ \ \bar{P_k}=A_k\hat{P_{k-1}}A^T_k+R \tag{7} $
第二步由观测方程,计算在某个状态下应该产生怎样的观测数据:
$ P(z_k|x_k)=N(C_kx_k,R) \tag{8} $
上述两步可归纳为:
- 预测
$ \bar{x_k}=A_k\hat{x_{k-1}}+u_k,\ \ \ \ \bar{P_k}=A_k\hat{P_{k-1}}A^T_k+R \tag{7} $
- 更新 先计算K(卡尔曼增益)
$ K=\bar{P_k}C^T_k(C_k\bar{P_k}C^T_k+R_k)^{-1} \tag{8} $
然后计算后验分布
$ \hat{x_k}=\bar{x_k}+K(z_k-C_k\bar{x_k}) \tag{9} $
$ \hat{P_k}=(I-KC_k)\bar{P_x} \tag{10} $
10.1.3 非线性系统和EKF
SLAM中的运动方程和观测方程通常是非线性函数,所以在非线性系统中,我们必须取一定的近似,将一个非高斯分布近似成高斯分布。我们希望把卡尔曼滤波器扩展到非线性系统中,称为扩展卡尔曼滤波(EKF)。
通常的做法是,在某个点附近考虑运动方程及观测方程的一阶泰勒展开,只保留一阶项,即线性的部分,然后按照线性系统进行推导。
偏导数F和H: $ F=\frac{\partial f}{\partial x_{k-1}},\ \ \ \ H=\frac{\partial h}{\partial x_{k}} \tag{11} $
卡尔曼增益$K_k$:
$ K_k=\bar{P}_kH^T(H\bar{P}_kH^T+Q_k)^{-1} \tag{12} $
后验概率:
$ \hat{x_k}=\bar{x_k}+K_k(z_k-h(\bar{x_k})) \tag{13} $
$ \hat{P_k}=(I-K_kH)\bar{P_k} \tag{14} $
10.2 BA与图优化
Bundle Adjustment简称为BA,是指从视觉重建中提炼出最优的3D模型和相机参数(内参数和外参数)。从每一个特征点反射出来的几束光线(bundles of light rays),在我们把相机姿态和特征点空间位置做出最优的调整(adjustment)之后,最后收束到相机光心的这个过程。
SLAM的研究者们通常认为包含大量特征点和相机位姿的BA计算量过大,不适合实时计算。直到近十年,人们逐渐认识到SLAM问题中BA的稀疏特性,才使它能够在实时的场景中应用
10.2.1 投影模型和BA代价函数
将世界坐标系中的点p投影到像素坐标的过程就是观测方程 $z=h(x,y)$,x为此时相机的位姿,即外参R,t ,它对应的李代数为$\xi$,路标y即这里的三维点p,而观测数据则是像素坐标 $z^\Delta =[u_s ,v_s]^T$。以最小二乘的角度来考虑,则此次观测的误差为 $e=z-h(\xi,p)$。
然后把其他时刻的观测量也考虑进来,可以给误差添加一个下标。设$z_{ij}$为在位姿$\xi_i$处观察路标$p_j$产生的数据,那么整体的代价函数(Cost Function)为:
$ \frac12\sum^m_{i=1}\sum^n_{j=1}||e_{ij}||^2=\frac12\sum^m_{i=1}\sum^n_{j=1}||z_{ij}-h(\xi_i,p_j)||^2 \tag{15} $
对这个最小二乘进行求解,相当于对位姿和路标同时做了调整,也就是所谓的BA。
10.2.2 BA的求解
因为观测模型$h(\xi,p)$不是线性函数,所以可以使用高斯牛顿法或列文伯格-马夸尔特法求解,即从某个初始值开始,不断地寻找下降方向$\Delta x$来找到目标函数的最优解,即不断地求解增量方程 $H\Delta x=g$ 中的增量$\Delta x$。
自变量为所有待优化的变量(16),当我们给自变量一个增量时,目标函数变为(17),其中$F_{ij}$表示整个代价函数在当前状态下对相机姿态的偏导数,而$E_{ij}$表示该函数对路标点位置的偏导。
$ x=[\xi_1,\dots,\xi_m,p_1,\dots,p_n]^T \tag{16} $
$ \frac12||f(x+\Delta x)||^2\approx\frac12\sum^m_{i=1}\sum^n_{j=1}||e_{ij}+F_{ij}\Delta\xi_i+E_{ij}\Delta p_j||^2 \tag{17} $
把相机位姿变量放在一起(18),把相机位姿变量放在一起(19),则式(17)可以简化表达如(20)。
$ x_c=[\xi_1,\xi_2,\dots,\xi_m]^T \in \mathbb{R}^{6m} \tag{18} $
$ x_p=[p_1,p_2,\dots,p_m]^T \in \mathbb{R}^{3n} \tag{19} $
$ \frac12||f(x+\Delta x)||^2=\frac12||e+F\Delta x_c+E\Delta x_p||^2 \tag{20} $
需要注意的是,该式从一个由很多个小型二次项之和,变成了一个更整体的样子。这里的雅可比矩阵E和F必须是整体目标函数对整体变量的导数,它将是一个很大块的矩阵,而里头每个小分块,需要由每个误差项的导数$F_{ij}$和$E_{ij}$“拼凑”起来。
然后,无论我们使用高斯牛顿法还是列文伯格—马夸尔特方法,最后都将面对增量线性方程:$H\Delta x=g$。高斯牛顿法和列文伯格—马夸尔特法的主要差别在于H是取$J^TJ$还是$J^TJ+\lambda I$的形式。由于我们把变量归类成了位姿和空间点两种,所以雅可比矩阵可以分块为$J=[F\ E]$。那么,以高斯牛顿法为例,则H矩阵为(21):
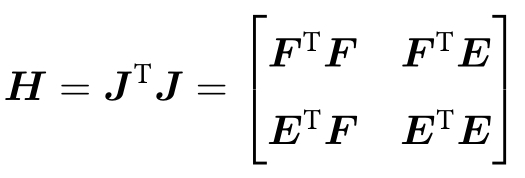
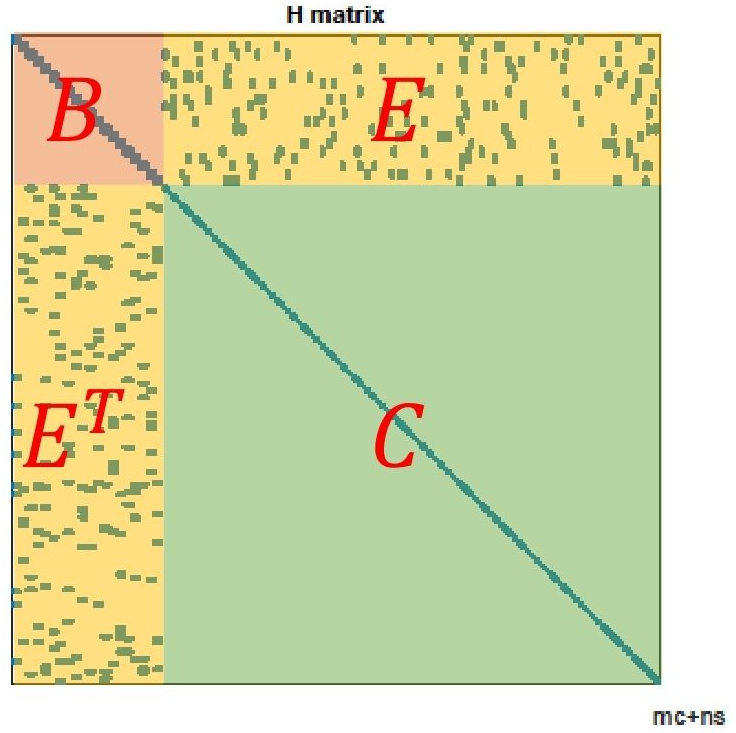
在视觉SLAM中,一幅图像有数百个特征点,大大增加了这个线性方程的规模。如果直接对H求逆来计算增量方程,由于矩阵求逆是复杂度为$O(n^3)$的操作,非常消耗计算资源。幸运的是,这里的H有一定的特殊结构,利用这个特殊结构可以加速求解过程。
10.2.3 稀疏性和边缘化
H矩阵的稀疏性是由雅可比矩阵$J(x)$引起的。考虑这些代价函数当中的其中一个$e_{ij}$。注意到,这个误差项只描述了在$\xi_i$看到$p_j$这件事,只涉及第i个相机位姿和第j个路标点,对其余部分的变量的导数都为0。所以该误差项对应的雅可比矩阵有下面的形式:
$ J_{ij}(x)=(O_{2\times 6},\dots,O_{2\times 6},\frac{\partial e_{ij}}{\partial \xi_i},O_{2\times 6},\dots,O_{2\times 3},\dots,O_{2\times 3},\frac{\partial e_{ij}}{\partial p_j},O_{2\times 3},\dots,O_{2\times 3}) \tag{22} $
其中$O_{2\times 6}$表示维度为2×6的0矩阵。该误差项对相机姿态的偏导$\frac{\partial e_{ij}}{\partial \xi_i}$维度为2×6,对路标点的偏导$\frac{\partial e_{ij}}{\partial p_j}$维度是2×3。这个误差项的雅可比矩阵,除了这两处为非零块之外,其余地方都为零。
将这些$J_{ij}$按照一定顺序列为向量,那么整体雅可比矩阵及相应的H矩阵的稀疏情况就如下所示
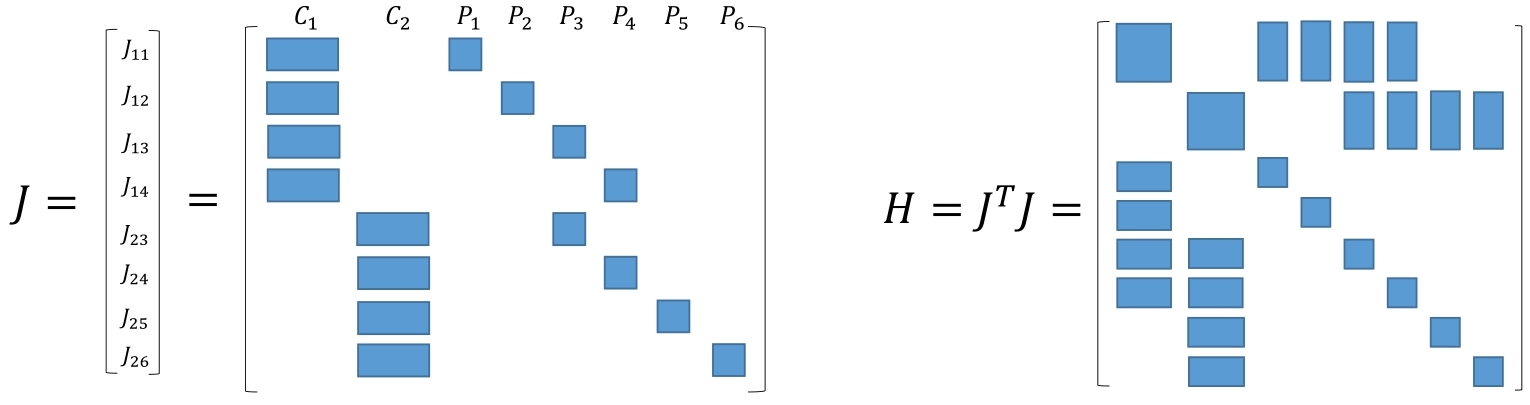
实际上存在着若干种利用H的稀疏性加速计算的方法,本节介绍视觉SLAM里一种最常用的手段:Schur消元,亦称为Marginalization(边缘化)。
首先将这个矩阵按照如下所示的方式做区域划分,这4个区域正好对应了公式(21)中的4个矩阵块。
于是,对应的线性方程组也可以由 $H\Delta x=g$ 变为如下形式:
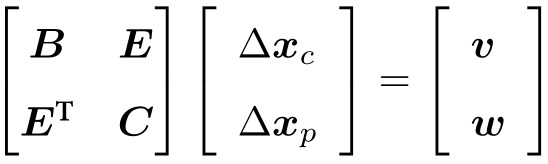
后面略。
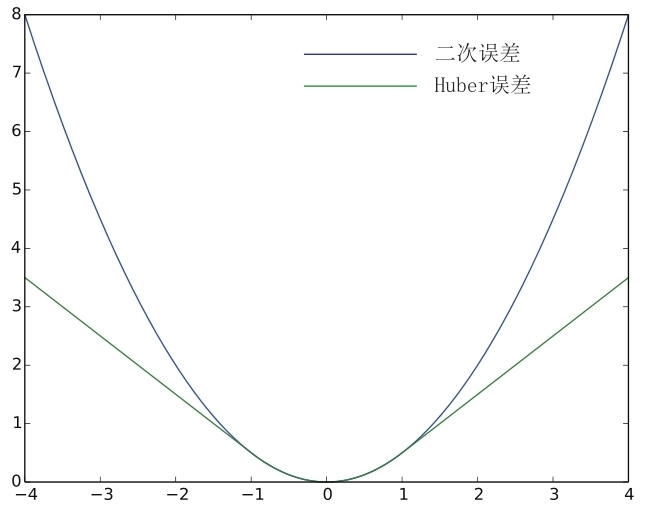
10.2.4 鲁棒核函数
当误差很大时,二范数增长得太快,核函数保证每条边的误差不会大得没边而掩盖掉其他的边。具体的方式是,把原先误差的二范数度量替换成一个增长没有那么快的函数,同时保证自己的光滑性质(不然无法求导!)。因为它们使得整个优化结果更为稳健,所以又叫它们鲁棒核函数(Robust Kernel)。
鲁棒核函数有许多种,例如最常用的Huber核: