第4讲 李群与李代数
4.1 李群与李代数基础
群是一种集合加上一种运算的代数结构。群要求运算满足以下条件(封结幺逆):
- 封闭性:$\forall a_1,a_2 \epsilon A,a_1\cdot a_2\epsilon A$
- 结合律:$\forall a_1,a_2,a_3 \epsilon A,(a_1\cdot a_2)\cdot a_3=a_1\cdot (a_2\cdot a_3)$
- 幺元:$\exists a_0\epsilon A,s.t.\forall a\epsilon A,a_0\cdot a=a\cdot a_0=a$
- 逆:$\forall a\epsilon A,\exists a^{-1}\epsilon A,s.t.a\cdot a^{-1}=a_0$
旋转矩阵SO(3)和变换矩阵SE(3),对加法是不封闭的(两个旋转矩阵的和不是旋转矩阵),对于乘法是封闭的(两个旋转矩阵的积是旋转矩阵)。
整数群的运算为加法:幺元为0,因为任意整数加0都不变;2的逆为-2,因为2+(-2)=0。
李群是指具有连续(光滑)性质的群。
像整数群Z那样离散的群没有连续性质,所以不是李群。
特殊正交群SO(3)和特殊欧氏群SE(3)
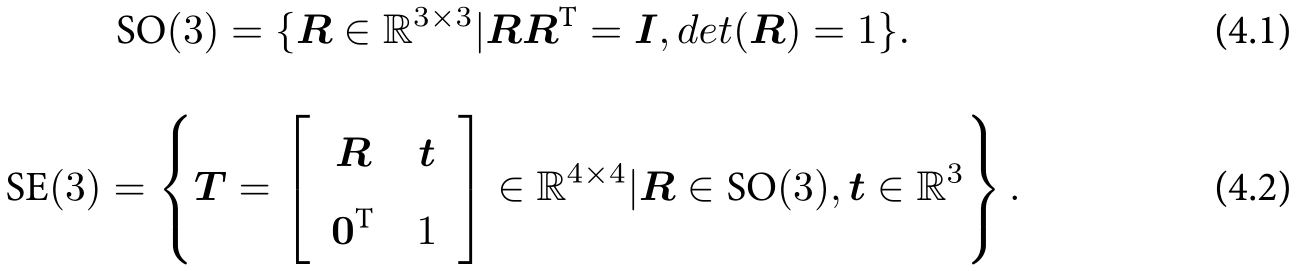
李代数由一个集合V,一个数域F,一个二元运算[ , ](李括号)组成。如果满足以下性质,则称$(V,F,[\ ,\ ])$为一个李代数,记作g。
- 封闭性:$\forall X,Y\epsilon V,[X,Y]\epsilon V$
- 双线形:$\forall X,Y,Z\epsilon V,a,b\epsilon F$,有$[aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[Z,X]+b[Z,Y]$
- 自反性:$\forall X\epsilon V,[X,Y]=0$
- 雅可比等价:$\forall X,Y,Z\epsilon V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0$
不要求结合律。
每个李群都有与之对应的李代数,李代数描述了李群的局部性质。李代数是李群的指数映射。
参考:最小二乘优化时需要求导,求导需要$x_i+\Delta x$,特殊正交群SO(3)对加法不封闭。然而,特殊正交群是李群的一种,因此我们可以将其映射为李代数来化乘为加,解决这个问题。李代数是李群的指数映射,而两个指数函数相乘是可以转化成加法操作的。
参考:李代数是李群在幺元处的正切空间,切空间本身是一个向量空间。什么叫“正切空间”?以不太严谨的例子来说明的话,李群就像一个无法定义加运算的曲面,对于曲面上的两点,相加后不一定还在这个曲面上。而李代数就像这个曲面对应的切面,在切线附近具有和原曲面相近的性质。就像我们可以用某个曲线的切线,来近似代替切点附近的曲线,进行一些操作。于是通过李代数,我们终于可以进行求导等操作了。
向量a变成反对称矩阵A,反对称矩阵A变成向量a:
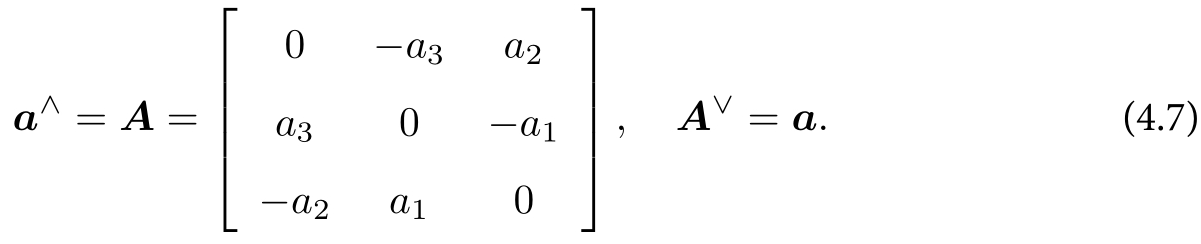
4.2 指数与对数映射
SO(3)上的指数映射即罗德里格斯公式:
$ exp(\theta a^\wedge)=cos\theta I+(1-cos\theta)aa^T+sin\theta a^\wedge \tag{1} $
SE(3)上的指数映射:
$ J=\frac{sin\theta}\theta I+(1-\frac{sin\theta}\theta)aa^T+\frac{1-cos\theta}\theta a^\wedge \tag{2} $
SO(3),SE(3),so(3),se(3)的关系:
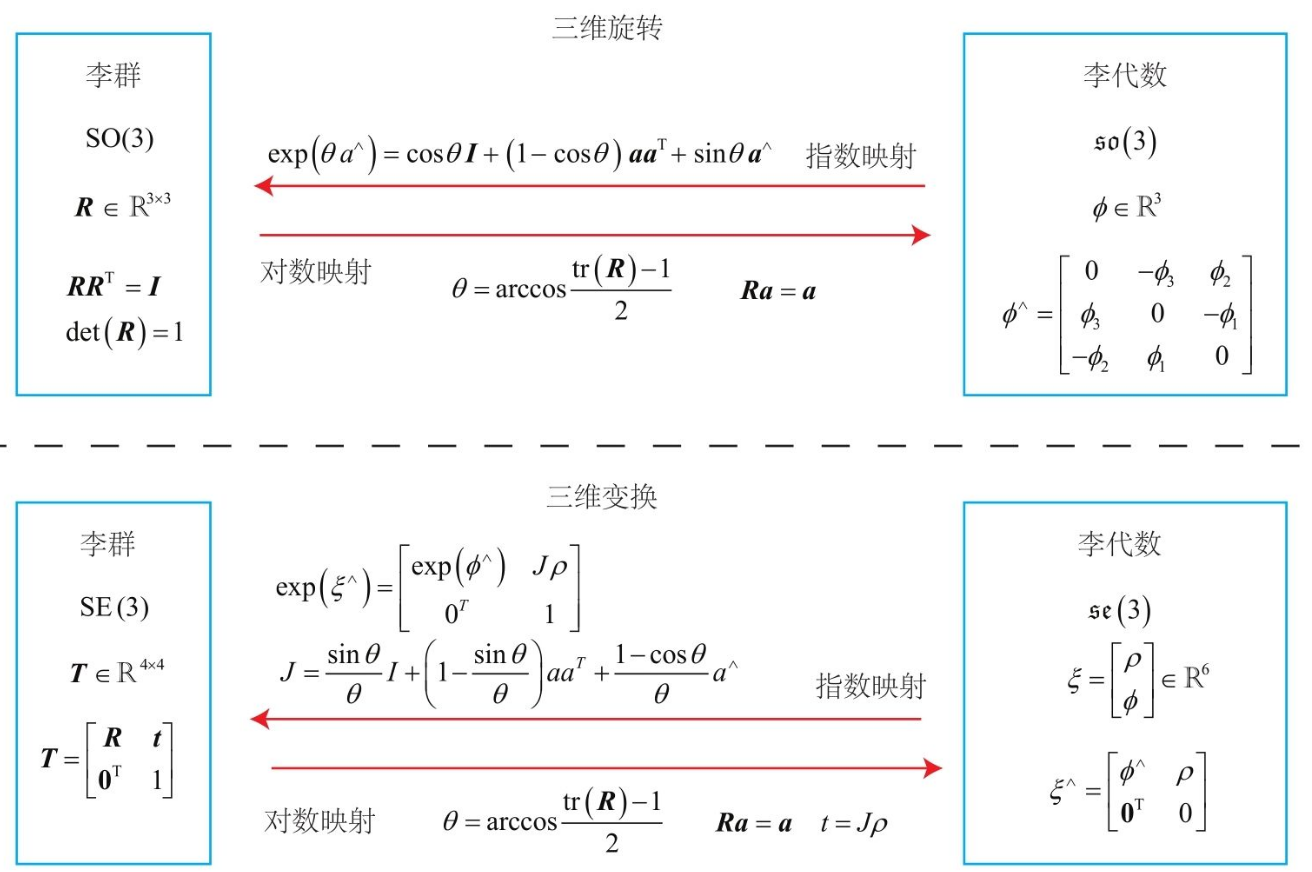
特殊正交群SO(3)的旋转矩阵R,通过指数映射,得到对应的李代数so(3)。
4.3 李代数求导与扰动模型
BCH公式(化乘为加):两个李代数指数映射的乘积,由Baker-Campbell-Hausdorff公式给出:
$ ln(exp(A)exp(B))=A+B+\frac12[A,B]+\frac1{12}[A,[A,B]]-\frac1{12}[B,[A,B]]+\cdots \tag{3} $
其中 [ ] 为李括号