第3讲 三维空间刚体运动
3.1 旋转矩阵
内积可以描述向量间的投影关系
$ a\cdot b=a^Tb=\sum^3_{i=1}a_ib_i=|a||b|cos<a,b> $
外积的方向垂直于这两个向量,大小为$|a||b|sin<a,b>$ ,是两个向量张成的四边形的有向面积
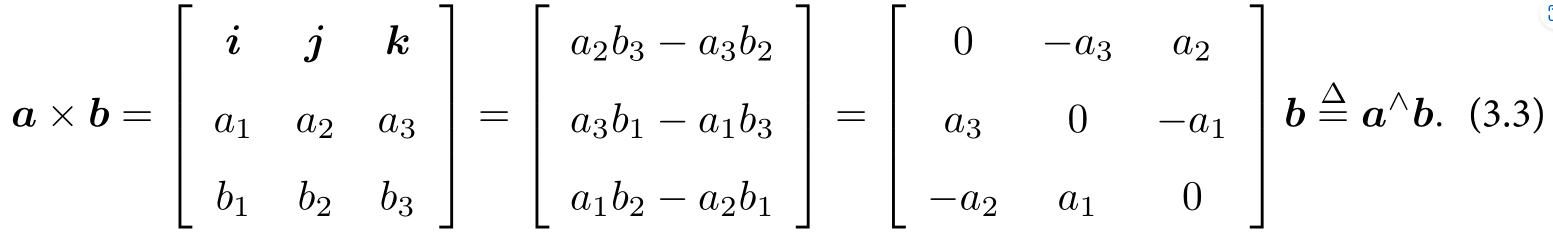
对于外积,我们引入了∧符号,把a写成一个矩阵。事实上是一个反对称矩阵(Skew-symmetric),你可以将∧记成一个反对称符号。这样就把外积 $a\times b$ 写成了矩阵与向量的乘法$a^∧b$ ,把它变成了线性运算。这个符号将在后文经常用到,请记住它。外积只对三维向量存在定义,我们还能用外积表示向量的旋转。
旋转矩阵R是一个行列式为1的正交矩阵。反之,行列式为1的正交矩阵也是一个旋转矩阵。所以,可以把旋转矩阵的集合定义如下:
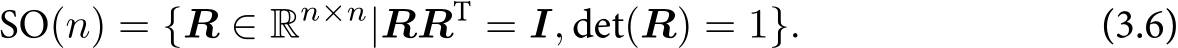
det(R)表示R矩阵的行列式(determinant),几何意义为列向量所围成的平行四边形的面积。
正交矩阵即逆为自身转置的矩阵。
SO(n)是特殊正交群(Special Orthogonal Group)。这个集合由n维空间的旋转矩阵组成,SO(3)就是三维空间的旋转。
变换矩阵T
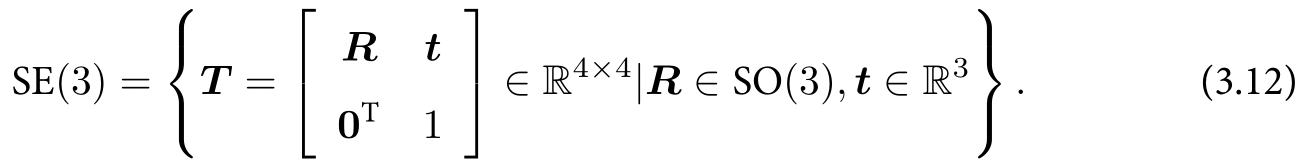
SE(n)是特殊欧式群(Special Euclidean Group)。
3.3 旋转向量和欧拉角
旋转向量(或轴角,Axis-Angle)的方向与旋转轴一致,长度等于旋转角。(任意旋转都可以用一个旋转轴和一个旋转角来刻画)
旋转向量转换为旋转矩阵:罗德里格斯公式(Rodrigues’s Formula)
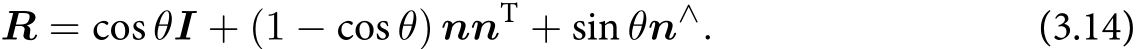
符号∧是向量到反对称的转换符,见式(3.3)
旋转矩阵转换为旋转向量:
转轴n是矩阵R特征值为1时对应的特征向量,求解$Rn=n$,再归一化,就得到转轴。转角$\theta$:

tr(R)为矩阵的迹,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹。
欧拉角的万向锁问题:在俯仰角为$\pm90^o$时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由3次旋转变成了2次旋转)。这被称为奇异性问题。(在其他形式的欧拉角中也同样存在)所以欧拉角不适用与插值和迭代,往往只用于人机交互中。
3.4 四元数
四元数:假设某个旋转时绕单位向量$n=[n_x,n_y,n_z]^T$进行角度为 $\theta$ 的旋转,那么其四元数形式为:
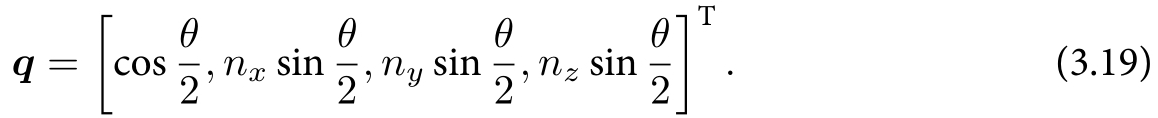
在四元数中,任意旋转都可以由两个互为相反数的四元数表示。
由单位四元数计算旋转轴和夹角:
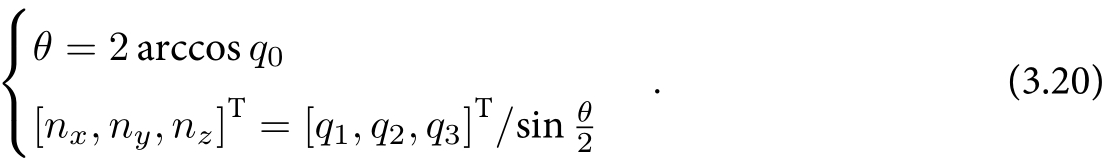
四元数转换为旋转矩阵:设四元数$q=q_0+q_1i+q_2j+q_3k$,对应的旋转矩阵R为:
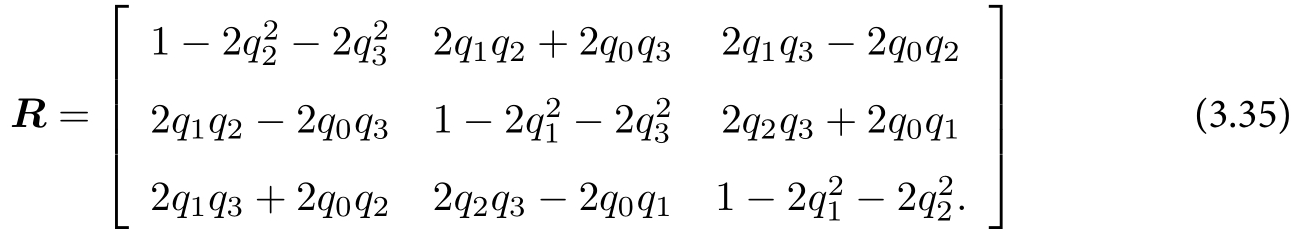
旋转矩阵转换为四元数:假设矩阵为$R={m_{ij}},i,j\epsilon[1,2,3]$,对应的四元数q为:
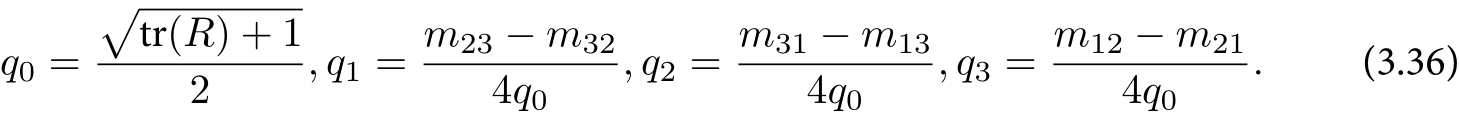
由于q 和-q 表示同一个旋转,事实上一个R 对应的四元数表示并不是唯一的。同时,除了上面给出的转换方式之外,还存在其他几种计算方法,而本书都省略了。实际编程中,当$q_0$接近0时,其余3个分量会非常大,导致解不稳定,此时我们再考虑使用其他的方式进行转换。
3.5 相似、仿射、射影变换
常见变换性质比较
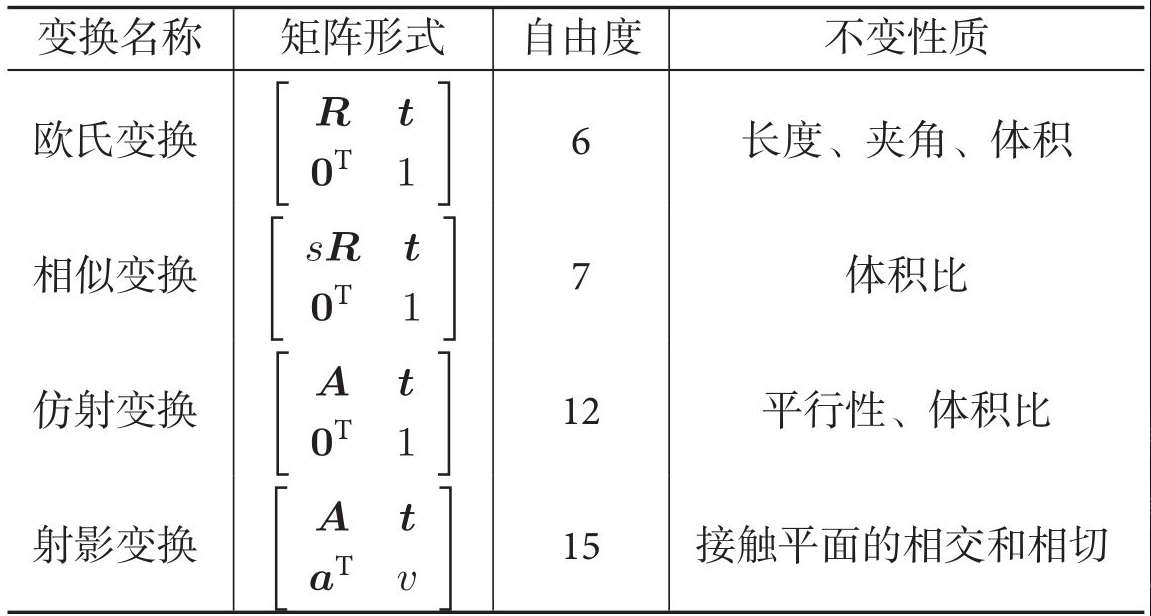
从真实世界到相机照片的变换是一个射影变换。如果相机的焦距为无穷远,那么这个变换为仿射变换。